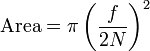Liczba f jest używana do wyrażenia ilości światła, które może uchwycić obiektyw, więc 85 mm f / 1,8 i 24 mm f / 1,8 mogą uchwycić tę samą ilość. Tutaj f to ogniskowa, a f / 1.8 oznacza, że ​​maksymalna średnica apertury to 47,2 mm w pierwszym przykładzie i 13,3 mm w drugim.

Należy tutaj wziąć pod uwagę że obiektyw 85 mm ma znacznie węższe pole widzenia, dlatego musi zbierać taką samą ilość światła ze znacznie mniejszego obszaru - aby skompensować wąski widok, przysłona musi być większa.

apertura musi być większa, jest liniowo skorelowana z ogniskową. Można powiedzieć, że obiektyw 24 mm z aperturą 13,3 mm może zebrać tyle samo światła, co obiektyw 85 mm z aperturą 47,2 mm, ale mówienie o liczbie F znacznie ułatwia to zauważenie.

Terminologia jest myląca, prawda?

Liczba f obiektywu f / 1.8 to po prostu 1.8 . Jest to określone jako N , a nie f . f to ogniskowa.

f / 1.8 dosłownie oznacza „ogniskową podzieloną przez N ”. Więc jeśli odniesiesz się do f / 1.8, to nie jest liczba f, to jest ogniskowa podzielona przez liczbę f.

Aby dokładniej wyjaśnić równania:

Drugie równanie mówi, że ogniskowa f podzielona przez średnicę apertury d to liczba f N . Lub f / N = d . Zatem f / 1,8 dosłownie oznacza „ogniskową podzieloną przez 1,8 (równa się średnicy).

Jeśli spojrzymy na górne równanie od f / N = d , to f / 2N musi wynosić d / 2 (a d / 2 to połowa średnicy, tak samo jak promień apertury). Wiemy, że obszar koła to pi r do kwadratu . Więc pi razy f / 2N do kwadratu to po prostu powierzchnia otworu przysłony.

Zatem jedno równanie mówi ci o średnicy otworu apertury, a drugie wykorzystuje podstawową geometrię do obliczenia obszaru otworu apertury, którym jest okrąg.

Myślę, że zamieszanie wynika z dwóch różnych rzeczy, które błędnie łączą się ze sobą jako „ilość światła”.

Rzeczywista ilość światła wpuszczanego przez obiektyw jest tylko funkcją pola przysłony. Ponieważ powierzchnia idzie w parze ze średnicą podniesioną do kwadratu, jest to proporcjonalne do kwadratu średnicy.

Jednak to, co jest bardziej istotne dla ekspozycji, to nie całkowita ilość światła, jaką może zebrać obiektyw, ale jasność zogniskowanego obrazu, który wytwarza. Tutaj w grę wchodzi ogniskowa. Powiedzmy, że masz obiektyw 100 mm z aperturą o średnicy 25 mm (lub regulowaną przysłoną ustawioną na 25 mm). Teraz porównaj to z obiektywem 200 mm. Jeśli obiektyw 200 mm ma również przysłonę 25 mm, to wpuści taką samą ilość światła. Jednak ta sama ilość światła pochodząca od obiektu jest teraz zogniskowana dwukrotnie, tym samym zajmując 4 razy większą powierzchnię. Oznacza to, że obiektyw 200 mm z przysłoną 25 mm tworzy obraz o 1/4 jaśniejszego (2 stopnie przysłony w dół) w porównaniu z obiektywem 100 mm z tą samą przysłoną 25 mm.

Zauważ, że jasność ostry obraz zmniejsza się do kwadratu ogniskowej, ale zwiększa się do kwadratu średnicy apertury. Oznacza to, że gdybyśmy wzięli stosunek tych dwóch, otrzymalibyśmy znormalizowaną miarę jasności zogniskowanego obrazu do celów ekspozycji. Ten stosunek jest dokładnie tym, czym są stopnie przysłony. Są one zwykle zapisywane jako f / n, na przykład f / 8,0 lub f / 11. To tylko wyrażenie. Pełne równanie to:

  aperture = focallength / n  

W pierwszym przykładzie obiektywu 100 mm z aperturą 25 mm, czyli:

  25mm = 100mm / 4  

Ponieważ pisanie i mówienie tego przez cały czas staje się kłopotliwe, a chodzi o to, aby nie musieć przejmować się absolutną ogniskową i aperturą Oznacza to, że jest to w skrócie „f / 4”, gdzie „f” oznacza ogniskową obiektywu, a „4” oznacza stosunek tej ogniskowej do średnicy apertury. Drugi przykład to:

  25mm = 200mm / 8

lub „f / 8”. Oprócz niewielkich strat światła i innych subtelnych efektów, które można zignorować przez większość czasu, jeden obiektyw z przysłoną ustawioną na f / 8 da taki sam obraz skupiony na jasności, jak inny obiektyw przy f / 8, niezależnie od ogniskowej. To wyjaśnia również, dlaczego długie soczewki mają zwykle większą średnicę. Obiektyw 50 mm potrzebuje jedynie przysłony 12,5 mm, aby uzyskać f / 4. Z drugiej strony obiektyw 300 mm wymaga przysłony o średnicy 75 mm, aby uzyskać taką samą jasność obrazu tego samego obiektu. Oznacza to, że podstawowa fizyka mówi, że obiektyw 300 mm musi mieć co najmniej 3 cale średnicy, aby uzyskać f / 4.

Co oznacza f w wartościach przysłony

f oznacza ogniskową obiektywu. Obiektyw f / 1.8 ma średnicę źrenicy wejściowej D = f / 1.8. Obiektyw 85 mm z przysłoną f / 1,8 będzie miał źrenicę wejściową o średnicy 85 / 1,8 = 47,2 mm. Soczewka 24 mm będzie miała średnicę źrenicy 24 / 1,8 = 13,3 mm. Ponieważ ilość światła przechodzącego przez soczewkę jest proporcjonalna do powierzchni źrenicy wejściowej, a ta ostatnia jest proporcjonalna do kwadratu jej średnicy, soczewka 85 mm najwyraźniej zbiera się

(47,2 / 13,3) ^ 2 = (85/24) ^ 2 = 12,5

razy więcej światła. Jednak ta uwaga dotyczy tylko ilości światła zebranego z każdego pojedynczego punktu obiektu, a nie całkowitej ilości światła docierającego z przestrzeni obiektu.

To samo f -liczba, ta sama ekspozycja (niezależnie od f lub D)

Jedną z rzeczy, które również wydawały mi się mylące, jest to, że ilość światła zebrana w czujnik z tym samym czasem otwarcia migawki dla różnych obiektywów o tej samej liczbie przysłony jest taki sam. Dlaczego jeden obiektyw jest wyraźnie większy od drugiego?

Oto ilustracja tego, co dzieje się w aparacie:

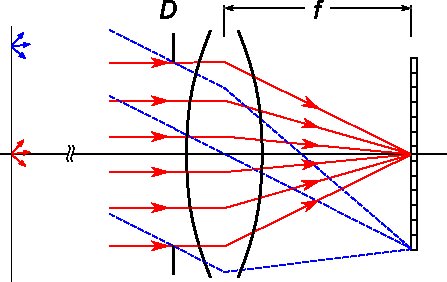
Dla uproszczenia, zakłada się, że obiekt znajduje się w nieskończoności, tak że wszystkie promienie z tego samego punktu obiektu zbliżają się równolegle do siebie. Czerwone stałe promienie docierają do soczewki równolegle do jej osi i wszystkie są skupione w środku kadru. Niebieskie przerywane promienie są równoległe do siebie, ale nie równoległe do osi. Wszystkie skupiają się na krawędzi kadru. Tak więc rozmiar ramki wraz z odległością ogniskową obiektywu determinują pole widzenia obiektywu.

(Zauważ, że skoro odległość od obiektu jest nieskończona, to pole widzenia w przestrzeni obiektu jest kątowy.)

Jeśli zmienimy obiektyw na taki o dłuższej ogniskowej przy zachowaniu tego samego rozmiaru oprawki, pole widzenia obiektywu maleje:

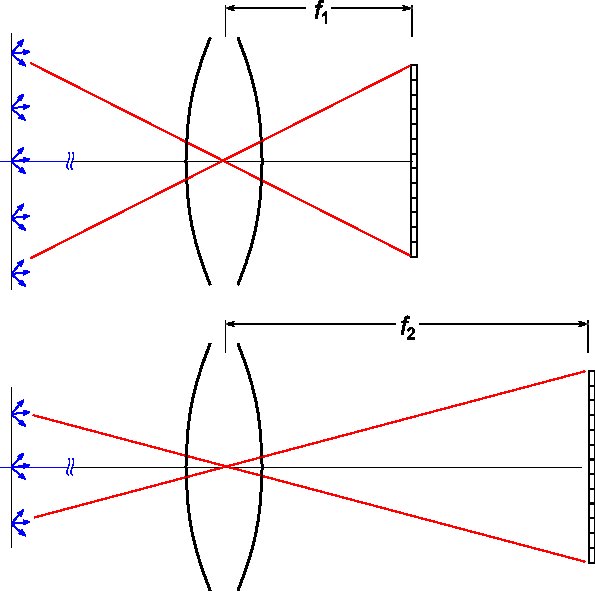
Zatem, podczas gdy soczewka wciąż zbiera taką samą ilość światła z każdego punktu w przestrzeni obiektu, rozmiar tej przestrzeni jest mniejszy, więc całkowita ilość światła docierającego do błony lub detektora jest zmniejszona .

Ta redukcja jest proporcjonalna do wzrostu ogniskowej, tj. ilość światła przy tym samym D jest zmniejszona o współczynnik (f2 / f1) ^ 2. (Jest do kwadratu, ponieważ musimy wziąć pod uwagę zmniejszenie pola widzenia w obu kierunkach.)

Jeśli teraz zwiększymy D o f2 / f1, ponownie zebrać starą ilość światła (ponieważ jest proporcjonalna do D ^ 2). Numer f zmieni się na: D2 / f2 = [D1 * (f2 / f1)] / f2 = D1 / f1. Dlatego jeśli chcemy zebrać taką samą ilość światła przy zmianie ogniskowej, musimy zachować stałą liczbę f.

Rozmiar klatki ma znaczenie

Ostatni interesujący parametr to rozmiar ramy. Weź kompaktowy aparat z takim samym obiektywem o liczbie przysłony, co pełnoklatkowa lustrzanka jednoobiektywowa. Jeśli rozmiar obiektywu i czujnika zostanie zmniejszony proporcjonalnie do ogniskowej, obie kamery będą miały takie samo pole widzenia. Kompaktowy aparat zbierze mniej światła niż lustrzanka, ponieważ ma mniejszy obiektyw. Jednak nadal będzie dawał tę samą wartość ekspozycji na czujniku, ponieważ ekspozycja to ilość światła na jednostkę powierzchni .

Jeśli oba aparaty mają tę samą rozdzielczość, ekspozycja będzie taka sama, ale rzeczywista ilość światła na każdy piksel będzie większa w przypadku większej lustrzanki, co spowoduje niższy poziom szumów.

Każdy obiektyw o świetle f / 2.8 powinien dostarczać taką samą ilość światła do aparatu. Niektóre obiektywy muszą jednak ciężej pracować, aby się tam dostać.

Nie jest to technicznie dokładne, ale znalazłem najlepszy sposób, aby zmierzyć się z liczbą przysłony zbytnio myśląc o tym jako o ilości światła Stracony. Więc przy f / 2.8 tracisz tylko 2,8 x ilość światła, podczas gdy przy f / 11 tracisz 11 x ilość światła. *

Obiektyw tele z natury radzi sobie z mniejszą ilością światła niż obiektyw szerokokątny. Więc im ciężej obiektyw musi pracować, aby uniknąć utraty światła, tym więcej szkła potrzebujesz, aby uchwycić jak najwięcej światła, więc możesz mieć obiektyw 55-250 f / 4-5,6, który waży około 1 funta i ma 6-8 cali, podczas gdy 70-200mm f / 2.8 waży 6 funtów i ma ponad 12 cali długości.

* To nie jest sposób, w jaki to działa z matematycznego punktu widzenia, ale może pomóc w praktycznym praktycznym zrozumieniu.